问题:
如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a 2+3ab+2b 2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在下面虚框中画出图形,并根据图形回答(2a+b)(a+2b)=______.
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a 2+5ab+6b 2.
①你画的图中需要C类卡片______张. 
②可将多项式a 2+5ab+6b 2分解因式为______.
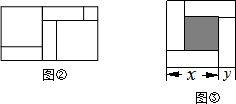
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式______(填写选项).
A.xy=
m2-n2
4
,B.x+y=m,C.x 2-y 2=m•n,D.x 2+y 2=
m2+n2
2
.
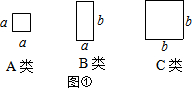
如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a 2+3ab+2b 2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在下面虚框中画出图形,并根据图形回答(2a+b)(a+2b)=______.
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a 2+5ab+6b 2.
①你画的图中需要C类卡片______张.
②可将多项式a 2+5ab+6b 2分解因式为______.

(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式______(填写选项).
A.xy=
,B.x+y=m,C.x 2-y 2=m•n,D.x 2+y 2=
.

比如图②可以解释为:(a+2b)(a+b)=a 2+3ab+2b 2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在下面虚框中画出图形,并根据图形回答(2a+b)(a+2b)=______.
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a 2+5ab+6b 2.
①你画的图中需要C类卡片______张.

②可将多项式a 2+5ab+6b 2分解因式为______.

(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式______(填写选项).
A.xy=
| m2-n2 |
| 4 |
| m2+n2 |
| 2 |

参考答案:
